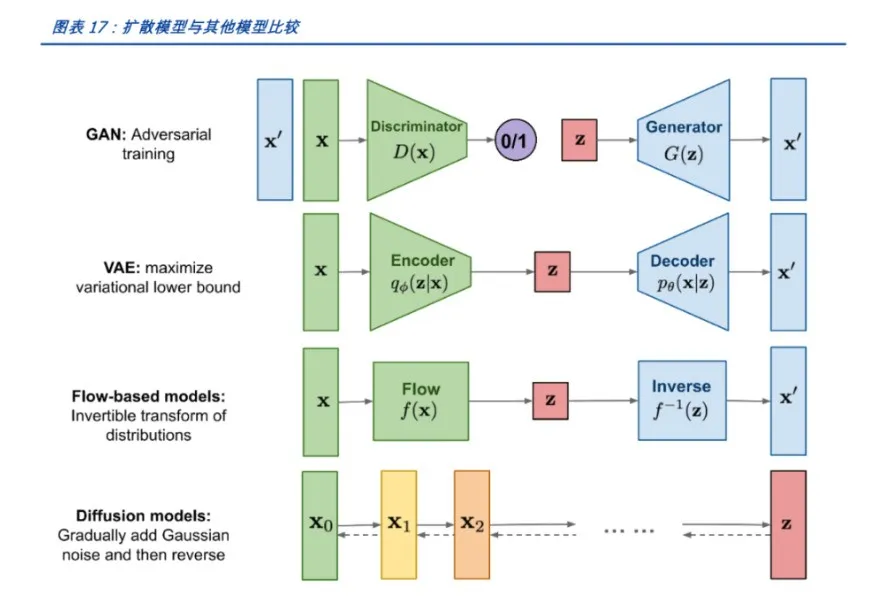
本文解析了五种深度生成模型,包括VAE、GAN、AR、Flow和Diffusion,详细讨论其原理与应用。
原文标题:必知!5大深度生成模型!
原文作者:数据派THU
冷月清谈:
怜星夜思:
2、在实际应用中,哪个深度生成模型更适合图像生成,为什么?
3、你如何看待生成对抗网络的训练不稳定问题?
原文内容

本文约5200字,建议阅读10分钟本文汇总了常用的深度学习模型,深入介绍其原理及应用。
-
编码器:将输入数据x编码为隐变量z的均值μ和标准差σ。
-
采样:从标准正态分布中采样一个ε,通过μ和σ计算z = μ + ε * σ。
-
解码器:将z解码为生成样本x'。
-
计算重构误差(如MSE)和KL散度,并优化模型参数以最小化两者的和。
-
能够生成多样化的样本。
-
隐变量具有明确的概率解释。
-
训练过程可能不稳定。
-
生成样本的质量可能不如其他模型。
-
数据生成与插值。
-
特征提取与降维。
Pythonimport torch import torch.nn as nn import torch.optim as optimclass VAE(nn.Module):
def init(self, input_dim, hidden_dim):
super(VAE, self).init()
self.encoder = nn.Sequential(
nn.Linear(input_dim, hidden_dim),
nn.ReLU(),
nn.Linear(hidden_dim, 2 * hidden_dim) # 均值和标准差
)
self.decoder = nn.Sequential(
nn.Linear(hidden_dim, hidden_dim),
nn.ReLU(),
nn.Linear(hidden_dim, input_dim),
nn.Sigmoid() # 二值数据,使用Sigmoid激活函数
)def reparameterize(self, mu, logvar):
std = torch.exp(0.5 * logvar)
eps = torch.randn_like(std)
return mu + eps * stddef forward(self, x):
h = self.encoder(x)
mu, logvar = h.chunk(2, dim=-1)
z = self.reparameterize(mu, logvar)
x_recon = self.decoder(z)
return x_recon, mu, logvar示例训练过程
model = VAE(input_dim=784, hidden_dim=400)
optimizer = optim.Adam(model.parameters(), lr=1e-3)假设x是输入数据,batch_size是批次大小
x = torch.randn(batch_size, 784)
recon_x, mu, logvar = model(x)
loss = nn.functional.binary_cross_entropy(recon_x, x, reduction=‘sum’) \
- 0.5 * torch.sum(torch.exp(logvar) + mu.pow(2) - 1 - logvar)
optimizer.zero_grad()
loss.backward()
optimizer.step()
-
判别器接受真实数据和生成器生成的假数据,进行二分类训练,优化其判断真实或生成数据的能力。
-
生成器根据判别器的反馈,尝试生成更加真实的假数据以欺骗判别器。
-
交替训练判别器和生成器,直到判别器无法区分真实和生成数据,或达到预设的训练轮数。
-
能够生成高质量的样本。
-
训练过程相对自由,不受数据分布限制。
-
训练不稳定,容易陷入局部最优。
-
需要大量的计算资源。
-
图像生成。
-
文本生成。
-
语音识别等。
Pythonimport torch import torch.nn as nn import torch.optim as optim判别器
class Discriminator(nn.Module):
def init(self, input_dim):
super(Discriminator, self).init()
self.fc = nn.Sequential(
nn.Linear(input_dim, 128),
nn.LeakyReLU(0.2),
nn.Linear(128, 1),
nn.Sigmoid()
)def forward(self, x):
return self.fc(x)生成器
class Generator(nn.Module):
def init(self, input_dim, output_dim):
super(Generator, self).init()
self.fc = nn.Sequential(
nn.Linear(input_dim, 128),
nn.ReLU(),
nn.Linear(128, output_dim),
nn.Tanh()
)def forward(self, x):
return self.fc(x)示例训练过程
discriminator = Discriminator(input_dim=784)
generator = Generator(input_dim=100, output_dim=784)
optimizer_D = optim.Adam(discriminator.parameters(), lr=0.0002)
optimizer_G = optim.Adam(generator.parameters(), lr=0.0002)
criterion = nn.BCEWithLogitsLoss()假设real_data是真实数据,batch_size是批次大小
real_data = torch.randn(batch_size, 784)
训练判别器
for p in discriminator.parameters():
p.requires_grad = True
for p in generator.parameters():
p.requires_grad = Falsenoise = torch.randn(batch_size, 100)
fake_data = generator(noise)
real_loss = criterion(discriminator(real_data), torch.ones_like(real_data))
fake_loss = criterion(discriminator(fake_data.detach()), torch.zeros_like(real_data))
discriminator_loss = real_loss + fake_loss
optimizer_D.zero_grad()
discriminator_loss.backward()
optimizer_D.step()训练生成器
for p in discriminator.parameters():
p.requires_grad = False
for p in generator.parameters():
p.requires_grad = True
noise = torch.randn(batch_size, 100)
fake_data = generator(noise)
gen_loss = criterion(discriminator(fake_data), torch.ones_like(real_data))
optimizer_G.zero_grad()
gen_loss.backward()
optimizer_G.step()
AR(自回归模型)
模型原理:
-
梯度消失与模型退化之困得以解决:Transformer模型凭借其独特的自注意力机制,能够游刃有余地捕捉序列中的长期依赖关系,从而摆脱了梯度消失和模型退化的桎梏。
-
并行计算能力卓越:Transformer模型的计算架构具备天然的并行性,使得在GPU上能够风驰电掣地进行训练和推断。
-
多任务表现出色:凭借强大的特征学习和表示能力,Transformer模型在机器翻译、文本分类、语音识别等多项任务中展现了卓越的性能。
-
计算资源需求庞大:由于Transformer模型的计算可并行性,训练和推断过程需要庞大的计算资源支持。
-
对初始化权重敏感:Transformer模型对初始化权重的选择极为挑剔,不当的初始化可能导致训练过程不稳定或出现过拟合问题。
-
长期依赖关系处理受限:尽管Transformer模型已有效解决梯度消失和模型退化问题,但在处理超长序列时仍面临挑战。
import torch import torch.nn as nn import torch.optim as optim #该示例仅用于说明Transformer的基本结构和原理。实际的Transformer模型(如GPT或BERT)要复杂得多,并且需要更多的预处理步骤,如分词、填充、掩码等。 class Transformer(nn.Module): def __init__(self, d_model, nhead, num_encoder_layers, num_decoder_layers, dim_feedforward=2048): super(Transformer, self).__init__() self.model_type = 'Transformer' # encoder layers self.src_mask = None self.pos_encoder = PositionalEncoding(d_model, max_len=5000) encoder_layers = nn.TransformerEncoderLayer(d_model, nhead, dim_feedforward) self.transformer_encoder = nn.TransformerEncoder(encoder_layers, num_encoder_layers) # decoder layers decoder_layers = nn.TransformerDecoderLayer(d_model, nhead, dim_feedforward) self.transformer_decoder = nn.TransformerDecoder(decoder_layers, num_decoder_layers) # decoder self.decoder = nn.Linear(d_model, d_model) self.init_weights() def init_weights(self): initrange = 0.1 self.decoder.weight.data.uniform_(-initrange, initrange) def forward(self, src, tgt, teacher_forcing_ratio=0.5): batch_size = tgt.size(0) tgt_len = tgt.size(1) tgt_vocab_size = self.decoder.out_features # forward pass through encoder src = self.pos_encoder(src) output = self.transformer_encoder(src) # prepare decoder input with teacher forcing target_input = tgt[:, :-1].contiguous() target_input = target_input.view(batch_size * tgt_len, -1) target_input = torch.autograd.Variable(target_input) # forward pass through decoder output2 = self.transformer_decoder(target_input, output) output2 = output2.view(batch_size, tgt_len, -1) # generate predictions prediction = self.decoder(output2) prediction = prediction.view(batch_size * tgt_len, tgt_vocab_size) return prediction[:, -1], prediction class PositionalEncoding(nn.Module): def __init__(self, d_model, max_len=5000): super(PositionalEncoding, self).__init__() # Compute the positional encodings once in log space. pe = torch.zeros(max_len, d_model) position = torch.arange(0, max_len).unsqueeze(1).float() div_term = torch.exp(torch.arange(0, d_model, 2).float() * -(torch.log(torch.tensor(10000.0)) / d_model)) pe[:, 0::2] = torch.sin(position * div_term) pe[:, 1::2] = torch.cos(position * div_term) pe = pe.unsqueeze(0) self.register_buffer('pe', pe) def forward(self, x): x = x + self.pe[:, :x.size(1)] return x # 超参数 d_model = 512 nhead = 8 num_encoder_layers = 6 num_decoder_layers = 6 dim_feedforward = 2048 # 实例化模型 model = Transformer(d_model, nhead, num_encoder_layers, num_decoder_layers, dim_feedforward) # 随机生成数据 src = torch.randn(10, 32, 512) tgt = torch.randn(10, 32, 512) # 前向传播 prediction, predictions = model(src, tgt)
print(prediction)

-
可以高效地进行样本生成和密度估计。
-
具有可逆性,便于反向传播和优化。
-
设计合适的可逆变换可能具有挑战性。
-
对于高维数据,流模型可能难以捕捉到复杂的依赖关系。
Pythonimport torch import torch.nn as nnclass FlowModel(nn.Module):
def init(self, input_dim, hidden_dim):
super(FlowModel, self).init()
self.transform1 = nn.Sequential(
nn.Linear(input_dim, hidden_dim),
nn.Tanh()
)
self.transform2 = nn.Sequential(
nn.Linear(hidden_dim, input_dim),
nn.Sigmoid()
)def forward(self, x):
z = self.transform1(x)
x_hat = self.transform2(z)
return x_hat, z
-
前向过程(Forward Process):从真实数据开始,逐步添加噪声,直到达到纯噪声状态。这个过程中,需要计算每一步的噪声水平,并保存下来。
-
反向过程(Reverse Process):从纯噪声开始,逐步去除噪声,直到恢复到目标数据。在这个过程中,使用神经网络(通常是U-Net结构)来预测每一步的噪声水平,并据此生成数据。
-
优化:通过最小化真实数据与生成数据之间的差异来训练模型。常用的损失函数包括MSE(均方误差)和BCE(二元交叉熵)。
-
生成质量高:由于Diffusion Model采用了逐步扩散和恢复的过程,因此可以生成高质量的数据。
-
可解释性强:Diffusion Model的生成过程具有明显的物理意义,便于理解和解释。
-
灵活性好:Diffusion Model可以处理各种类型的数据,包括图像、文本和音频等。
-
训练时间长:由于Diffusion Model需要进行多步的扩散和恢复过程,因此训练时间较长。
-
计算资源需求大:为了保证生成质量,Diffusion Model通常需要较大的计算资源,包括内存和计算力。
import torch import torch.nn as nn import torch.optim as optim定义U-Net模型
class UNet(nn.Module):
…省略模型定义…
定义Diffusion Model
class DiffusionModel(nn.Module):
def init(self, unet):
super(DiffusionModel, self).init()
self.unet = unetdef forward(self, x_t, t):
x_t为当前时刻的数据,t为噪声水平
使用U-Net预测噪声水平
noise_pred = self.unet(x_t, t)
根据噪声水平生成数据
x_t_minus_1 = x_t - noise_pred * torch.sqrt(1 - torch.exp(-2 * t))
return x_t_minus_1初始化模型和优化器
unet = UNet()
model = DiffusionModel(unet)
optimizer = optim.Adam(model.parameters(), lr=0.001)训练过程
for epoch in range(num_epochs):
for x_real in dataloader: # 从数据加载器中获取真实数据前向过程
x_t = x_real # 从真实数据开始
for t in torch.linspace(0, 1, num_steps):添加噪声
noise = torch.randn_like(x_t) * torch.sqrt(1 - torch.exp(-2 * t))
x_t = x_t + noise * torch.sqrt(torch.exp(-2 * t))计算预测噪声
noise_pred = model(x_t, t)
计算损失
loss = nn.MSELoss()(noise_pred, noise)
反向传播和优化
optimizer.zero_grad()
loss.backward()
optimizer.step()